Nongradient optimization techniques (Nelder-Mead and Rosenbrock)

The assembly available for download on this site contains two nongradient optimization techniques: Rosenbrock and Nelder-Mead.

Download Optimization.NET (.NET 6.0 / Nunit 3.0)

Rosenbrock algorithm

The Rosenbrock method is a 0th order search algorithm and it does not require gradient of the target function. Only simple evaluations of the objective function are used. Yet, this algorithm approximates a gradient search thus combining advantages of 0th order and 1st order strategies.

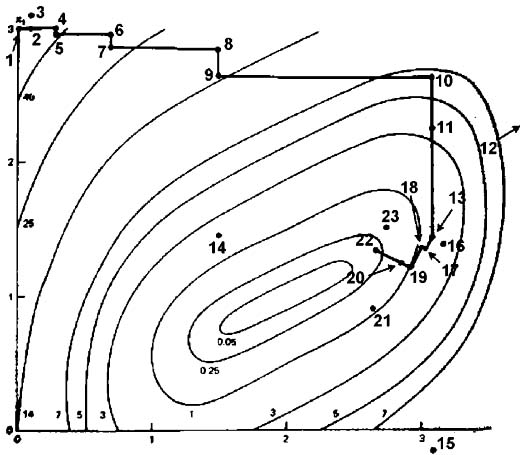
In the first iteration, it is a simple 0th order search in the directions of the base vectors of an n-dimensional coordinate system (in the figure above n=2). In the case of a success, which is an attempt yielding a new minimum value of the target function, the step width is increased, while in the case of a failure it is decreased and the opposite direction will be tried (see points 1 to 16 in the figure above). Once a success has been found and exploited in each base direction, the coordinate system is rotated in order to make the first base vector point into the direction of the gradient (the points 13,16,&17 are defining the new base in the figure above). Now all step widths are initialized and the process is repeated using the rotated coordinate system (points 16 to 23). The creation of a new rotated coordinate system is usually done using a Gram-Shmidt orthogonalization procedure. In extreme cases, this algorithm becomes numerically instable. This instabillity can lead to a premature ending of the optimization algorithm. The Gram-Shmidt orthogonalization procedure can also become very time consuming when the dimension n of the search space increases (the complexity of the procedure is n^3). The new orthogonalization procedure of J.R.Palmer solves these issues.

Nelder Mead Algorithm

A direct search method of optimization that works moderately well for stochastic problems. It is based on evaluating a function at the vertices of a simplex, then iteratively shrinking the simplex as better points are found until some desired bound is obtained (Nelder and Mead 1965). The Nelder-Mead method is a simplex method for finding a local minimum of a function of several variables. It's discovery is attributed to J. A. Nelder and R. Mead. For two variables, a simplex is a triangle, and the method is a pattern search that compares function values at the three vertices of a triangle.

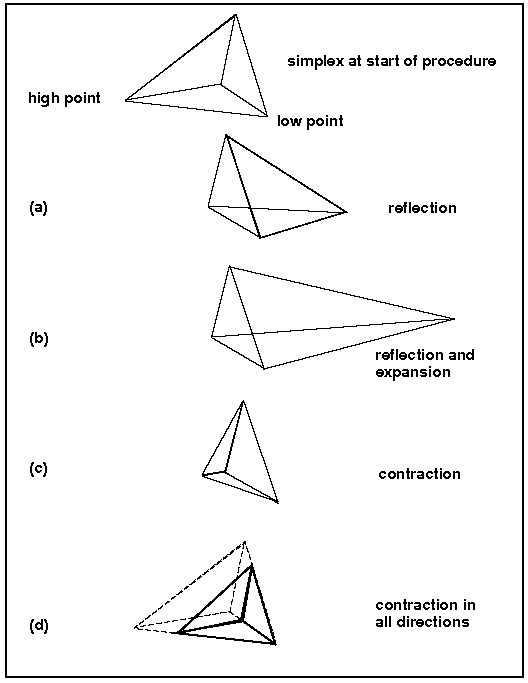
As its ilustrated on the figure above the worst vertex, where f(x,y) is largest, is rejected and replaced with a new vertex. A new triangle is formed and the search is continued. The process generates a sequence of triangles ( which might have different shapes), for which the function values at the vertices get smaller and smaller. The size of the triangles is reduced and the coordinates of the minimum point are found. The algorithm is stated using the term simplex (a generalized triangle in n dimensions) and will find the minimum of a function of n variables.

Comparison of Nelder-Mead and Rosenbrock

Although the Nelder-Mead is compast and elegenat an d can be effective in many cases, in general it should be avoided as a standalone solution because there is no proof of convergence for it. In fact, Nelder-Mead can fail to find a local optimum of a very simple optimization problem based on the minimization of a polynomial. This is due to degenerescence inside the simplex. Even when no degenerescence occurs, the convergence speed can becomes arbitrarly slow. The Rosenbrock algorithm does not suffer from these problems and has been proven to always converge to at least local minimum.