C60 Orientational Ordering in Superconducting Na2RbC60
Krzysztof Kniaz , John E. Fischer, Qing Zhu
Department of Materials Science and Engineering and Laboratory for Research on the Structure of Matter, University of Pennsylvania, Philadelphia PA 19104-6272
Matthew J. Rosseinsky, Donald W. Murphy and Otto Zhou
AT&T Bell Laboratories Murray Hill, New Jersey 07974-2070
The solid state properties of fullerenes and their intercalation compounds continue to attract considerable interest. Pristine C60 undergoes an orientational ordering transition at 260 K which involves a lattice transformation from face-centered cubic (fcc) at high T to simple cubic (sc) at low T. In the latter, the molecular orientations are fixed by interactions with nearest neighbors such that the C-C overlap between neighboring molecules is minimized by bringing electron-rich and electron-poor regions of adjacent C60 molecules into contact. Solid C60 intercalated by large alkalis (K, Rb) remains fcc in the merohedrally disordered, superconducting M3C60 phases. Saturation doping to M6C60 produces the ordered body-centered cubic (bcc) structure. In contrast, Na intercalation leads to derivatives with different properties, for example with small sodium clusters in octahedral voids of the fcc lattice. Furthermore, none of the Na-intercalated phases superconduct, despite having the ``right'' structure and lattice constant. Recently it was discovered that compounds with a low level of Na-doping (NaxC60, 1 < x <3) undergo fcc to sc transitions upon cooling, similar to pristine C60.
``Mixed'' intercalation with a heavy alkali plus sodium yields the ternary compounds Na2KC60, Na2RbC60 and Na2CsC60. The latter is fcc, space group Fm-3m with merohedral disorder (defined below), just like the binary superconductors M3C60 (M = K or Rb), and exhibits a superconducting onset Tc and lattice constant a which are consistent with a universal curve. The former is fcc at 300 K but phase separates at low T and/or high pressure, most probably into NaxC60 and K3C60. Na2RbC60 remains single phase fcc but only becomes superconducting at an anomalously low Tc of 4-5 K (the universal curve would predict a Tc of 10-12 K), which has been attributed in a recent work to excess orientational disorder relative to the other fullerene superconductors. These authors base their conclusion on intensity analyses of low-resolution x-ray powder profiles, from which they claim a better fit to a model of complete orientational disorder (spherical shells), as opposed to the usual merohedral disorder in which the molecules are frozen at random into one of two standard orientations differing by a 90 deg rotation about a (100) direction. The purpose of this Communication is to show that in fact Na2RbC60 exhibits an unusually high degree of orientational order, and thus the low Tc of this compound cannot be attributed to excess disorder.
Our sample was synthesized by reacting Na5Hg with Rb6C60. X-ray powder diffraction patterns were recorded at beamline X7A at the Brookhaven NSLS with a Ge(111) channel-cut monochromator, flat Ge(220) analyer and a NaI:Tl scintillation detector. Data were collected with 0.01 deg steps and wavelng.= 0.90333 Angstr. at 27 K and with 0.005 deg steps using wavelng.= 0.70093 Angstr at 298 K. The 27 K data are shown as the dots in Figure 1; the solid curve is the final Rietveld refinement, which we arrived at as follows. Initially, we obtained a poor result, R(p)=18%, assuming the Fm-3m space group, i.e. merohedral disorder. A slightly better result, R(p)=15.2%, was obtained by modeling the C60 molecules as uniform spherical shells of charge. It should be noted however, that if indeed the fullerene molecules were completely disordered, application of hydrostatic pressure should drive them into a more ordered configuration, which in turn would enhance Tc according to Hirosawa et al. . In fact our sample remained non-superconducting above 4.5 K at pressures up to 5 kbar.
The final 27 K refinement shown in the figure below was obtained in space group Pa-3, motivated by direct observation of weak but significant reflections which are uniquely indexable as sc, labelled by (+) in the inset.
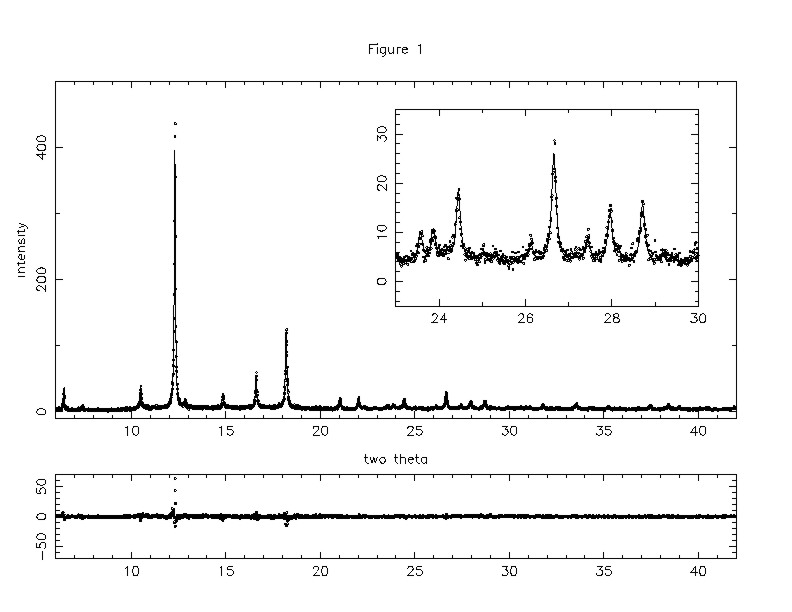
We obtain a = 14.0205(3) Angstr and a high degree of chemical ordering, with the larger Rb cations preferentially occupying octahedral sites and the smaller Na in tetrahedral sites. The final R(p) = 12.9%, significantly better than was obtained by assuming merohedral disorder or sperical shells. We first constrained all molecules to have the same orientation, specified by aligning two-fold molecular axes with cartesian crystal axes (which aligns pseudo three-fold molecular axes with (111) directions, then optimizing the ``setting angle'' phi by allowing rotations about (111). (We point out that the two standard orientations of the merohedrally-disordered structure correspond to phi = 0deg and 90deg.) This optimization revealed a global and double local minima in R(p) vs. phi at 24-26 deg (R(p)=13.6%) and 65 deg plus 105 deg (14.5%) respectively. This is very similar to what occurs in low-concentration Na-intercalated compounds, the only difference being that the double local minima are more pronounced in the latter system. For the final refinementwe chose to represent the double local minima as a single broad secondary minimum at 85deg. Thus in the final refinement we constrained all the molecules to either phi = 25 deg or phi = 85 deg and optimized the fractional populations. At 27 K we obtained an 80:20 admixture of global and local minima, essentially the same as the quenched disorder exhibited by pure C60 below. A calculation by Yildirim et al. shows that the orientational potential in NaxC60 closely mimics the behavior of R(p) vs. phi. Evidently the only important effect of the octahedral Rb in the present compound is to dampen the secondary minima, consistent with the small lattice constant which indicates that the octahedral Rb exerts negligible chemical pressure on the fcc structure.
The same approach was also found to be the best in refining the 298 K data, R(p)=9.5% with a 55:45 ratio of molecules in global and local minima respectively. The chemial ordering of octahedral Rb and tetrahedral Na is largely maintained at 298 K. Again similar to NaxC60, the sc peaks are considerably weaker at 298 K. By analogy to the Na results, we would expect the population of the global minimum to vanish in a first-order transition at 50-100 deg C. Despite the weak sc intensities, other models still gave poorer results, namely R(p)=11.5% for spherical shells and R(p)=15.6% for Fm-3m respectively.
Competition between C60--C60 and M^(+)--C60 interactions plays a key role in the structural properties of fullerene intercalation compounds. For example, large cations (K, Rb, Cs) in the (smaller) tetrahedral intersticies of the fcc lattice result in strong repulsive interactions due to the overlap of carbon and cation orbitals. These are minimized by orienting the molecules in one of the two standard orientations, because in these orientations the tetrahedral site has maximum volume and the C atoms are maximally distant from the cation centers. Since this short-range interaction can be minimized by two different orientations, random merohedral disorder is favored. This is no longer true with small tetrahedral cations such as Na^{+}; now the C60--C60 interactions, modified by the presence of Na^{+}, become dominant which favors the Pa-3 structure with ideal phi value of 22.4 deg. In ternary compounds the competition between large and small cations is in principle more complicated, and the phenomenon of orientational order in these compounds is just beginning to be studied. Apparently the structure of Na2CsC60 is determined by repulsion between C60's and the large octahedral Cs cations such that quenched merohedral disorder is again favored, consistent with the observation that this compound has a ``normal'' Tc and a. It is quite obvious that the orientations in both Na2RbC60 and dilute NaxC60 are defined by the combination of C60--C60 interactions and Coulomb repulsion, the octahedral Rb playing only a secondary role. It would be interesting to determine the detailed rotational dynamics of these compounds, in particular to find out the extent to which they resemble the dynamics of the isostructural pure C60. Another interesting open question is whether or not the low-T instability of Na2KC60 is somehow connected to the even smaller octahedral K^{+}. A final challenge for theory is to explain the unusually low critical temperature in orientationally-ordered Na2RbC60.
We acknowledge helpful discussions with T. Yildirim. The Penn contribution to this work was supported by the National Science Foundation MRL Program under Grant No. DMR91-20668 and by the Department of Energy, DE-FC02-86ER45254 and DE-FG05-90ER75596. The NSLS at Brookhaven was also supported by DOE, Division of Materials Sciences, DEAC02-76CH00016.
References
- P. A. Heiney, J. E. Fischer, A. R. McGhie ,W. J. Romanow, A. M. Denenstein, J. P. McCauley, Jr., A. B. Smith III and D. E. Cox, Phys. Rev. Letters 66, 2911 (1991).
- W. I. F. David, R. M. Ibberson, R. M. Matthewman, K. Prassides, T. J. Dennis, J. P. Hare, H. W. Kroto, R. Taylor, D. R. M. Walton, Nature 353, 147 (1991).
- P. W. Stephens, L. Mihaly, P. L. Lee, R. L. Whetten, S.-M. Huang, R. B. Kaner, F. Diederich, K. Holczer, Nature 351, 632 (1991).
- Q. Zhu, O. Zhou, N. Coustel, G. B. M. Vaughan, J. P. McCauley, Jr., W. J. Romanow, J. E. Fischer, A. B. Smith III, Science 254, 545 (1991).
- O. Zhou, J. E. Fischer, N. Coustel, S. Kycia , Q. Zhu, A. R. McGhie ,W. J. Romanow, J. P. McCauley, Jr., A. B. Smith III and D. E. Cox, Nature 351, 462 (1991).
- M. J. Rosseinsky, D. W. Murphy, R. M. Fleming, R. Tycko, A. P. Ramirez, T. Siegrist, G. Dabbagh, S. E. Barrett, Nature 356, 416 (1992).
- T. Yildirim, O. Zhou, J. E. Fischer, N. Bykovetz, R. M. Strongin, M. A. Cichy, A. B. Smith III, C. L. Lin and R. Jelinek, Nature 360 , 568 (1992).
- T. Yildirim, J. E. Fischer, A. B. Harris, P. W. Stephens, D. Liu, L. Brard, R. M. Strongin and A. B. Smith III, Phys. Rev. Lett. submitted.
- J. E. Shirber, D. L. Overmyer, W. R. Bayless M. J. Rosseinsky, D. W. Murphy, Q. Zhu, O. Zhu, K. Kniaz, J. E. Fischer, J. Phys. Chem. Solids (in press).