Analytic Hierarchical Process.NET
Download AHP.NET (.NET 4.5.1)
The Analytic Hierarchy Process is a solution / theory that is part of the Operations Research - a branch of economics that attempts to apply modeling and statistics to decision selection and execution of decisions within the enterprise. The AHP was proposed by Thomas Saaty who developed it while at the US Disarment Agency and the Wharton School, UPenn.
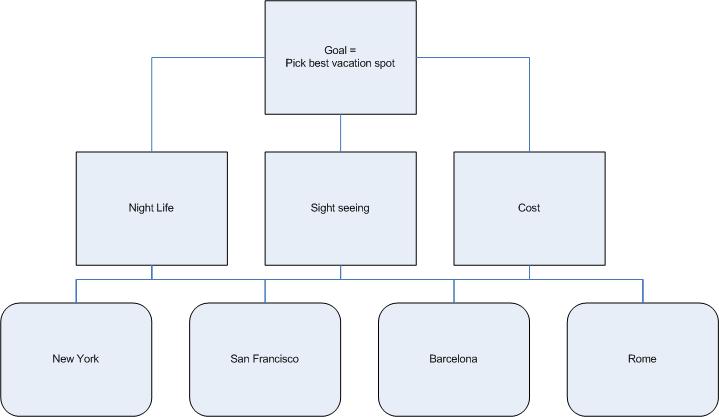
Let me illustrate the AHP with the following example: Imagine you are deciding on a vacation spot out of 4 choices A,B,C,D (for instance SF, NY, Rome and Barcelona) and using three criteria 1,2,3 (for example cost, night life and sightseeing). According to AHP to make a rational decision you should build a model as shown on the figure below in which the goal rests on selection criteria which depend on choices.
Selection of preferences for both criteria and choices is done via pair-wise comparison. Saaty proposed 9 grade value scale to compare choices in the model. Scale ranges from 1 (equal weight) to 9 (where one option is extremely more preferable than the other). After carrying out pair-wise comparisons on criteria with respect to the goal and then choices with respect to each criterion one obtains a matrix representation of the model (aka the decision matrix). The choice is then calculated using linear algebra transformation of the decision matrix. Consistency of the selection and the judgements involved is derived from the estimation of the eigenvalue of the decision matrix.
The preference selection is shown below:
We want evaluate our vacation spots with respect to sightseeing. We perform a pairwise comparison between Barcelona and the rest of spots, then Rome and finally NYC. Note that number of judgements that are required diminishes with every selection: user starts with 3 unique comparisons for Barcelona, then only 2 for Rome (because the Rome to Barcelona is inverse of Barcelona to Rome) and only one for SF. In the matrix below A=Barcelona, B=Rome, C=NY, D=SF. In this example we judge Rome to be more preferable that Barcelona, much more preferable than NY and we find that SF is as equally less preferable to Rome as Barcelona. Our preferences are summarized in the matrix below:

In the next step we normalize each matrix element by the sum of elements in each column and we calculate the sum for each row:
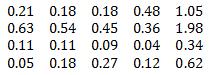
After that we normalize the sum of the rows, which yields:
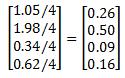
So the resulting priority matrix tells us that with respect to the criterion 3 (sightseeing) Rome has the highest priority. The final step in obtaining the preference of choices is to calculate the consistency ratio of the selection, which according to Saaty should be less or equal to 10% (according to his famous rule of thumb the consistency or uncertainty of the decision should be order of magnitude less than decision). First step in calculation of the consistency ratio is the calculation of the consistency index (which according to Saaty is the max eigenvalue of the comparison matrix) which is done as follows:
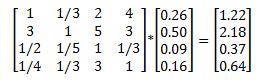
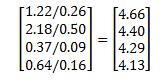
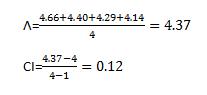
Where 4 stands for the dimension of the comparison matrix. Finally Consistency Ratio CR is a result of the division of our consistency index by the random index (consistency index of the totally random matrix – those values have been calculated up to 15th dimension):
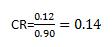
This value is bigger that 10% but still borderline acceptable.
To create full AHP model you should repeat the above step for all criteria and then in the final step arrive at the synthesis by multiplying preferences for all criteria times choice selections within each criteria.
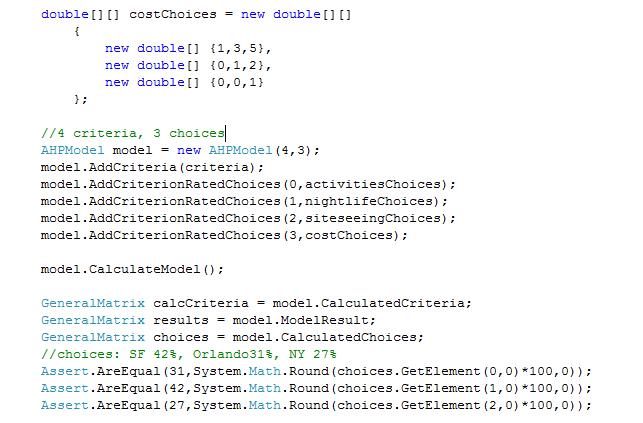
The use of the AHP component is illustrated by the code snippet below. My AHP implementation assumes that the pairwise comparison of criteria and choices has been already done and that the results can be expressed in the matrix form. I should add here that I'm using the General Matrix package for the linear algebra operations. The package is also available on this site.